Annuity Payment Formula for Calculation
The annuity payment formula is the equation used to calculate the periodic payment on an annuity, typically used for ordinary annuities.
Finding the correct annuity payments are very important in order to ensure loans are paid within the time frame specified. For example, when an individual receives a loan, they must pay a certain amount for a certain period of time. In order to determine these factors, an annuity payment formula is used. An annuity is defined by a series of periodic payments that are fully received at a later date. The initial payout of the loan is known as the present value. The original payment on an amortized loan can be valued as the PV.
Annuity Payment Formula
When using this ratio, it is understood that the rate does not change. The payments are scheduled to be at the same exact value. This formula also assumes that the first payment is one installment away. An annuity that grows at a proportional and consistent rate would use the formula as well. If the annuity changes the overall payment or rate, it must be adjusted each time. This is an important factor to note as it can change the periodic payments and other terms of the loan.
We have two important equation here:
Periodic payment formula when Present Value is known :
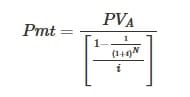
Periodic payment formula when Future Value is known :
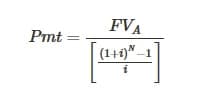
where are :
The annuity payment formula can be used for a range of different types of loans. Some of the most common scenarios used with the annuity payment formula are amortized loans, income annuities, lottery payouts as well as structured settlements. Constant period payments can easily use this formula in order to generate a successful and reliable method. It is also important to note that the rates are calculated per period. Calculating rates per period is a unique strategy used in the formula. Rate per period and number per period should always reflect exactly how often payments are made. When the rates and numbers reflect the per period statistics, the loan is more structured and accurate. For example, if the payments are made more frequently, the rate and number are subject to decrease. In contrast, if the payments are made less frequently, the rate and number are subject to increase as a result.
The annuity payment can be easily determined by fully rearranging the present value of the annuity formula. Rearranging the formula and solving for ‘P” is an important step in solving the equation. It is also important to note that the equation can be furthered simplified by multiplying the numerator by the reciprocal. When the numerator is multiplied by the reciprocal, the formula can be solved easier and is simplified in order to determine the annuity payments. As stated previously, some of the most common uses for annuity payments are lottery payouts, income annuities and different types of amortized loans. Any type of structured settlement can take advantage of periodic payments.
If the payments are increased in frequency, it will affect the other payments scheduled to take place in the future. Therefore it is important to take all of these factors into consideration. If the payments change as a result of larger payments made earlier in the loan term, other payments may not be needed frequently.
He is an expert in financial niche, long-term trading, and weekly technical levels.
The primary field of Igor's research is the application of machine learning in algorithmic trading.
Education: Computer Engineering and Ph.D. in machine learning.
Igor regularly publishes trading-related videos on the Fxigor Youtube channel.
To contact Igor write on:
igor@forex.in.rs
Related posts:
- What is Growing Annuity Payment ?
- FV Annuity with Continuous Compounding
- Present Value of Growing Annuity
- How to calculate number of periods for an annuity ?
- Future Value of Growing Annuity
- Present Value Annuity Factor
- The Remaining Balance Formula
- Can You Roll an Annuity Into an IRA? – Annuity Rollover Rules
- What is Equivalent Annual Annuity?
- How to Find n in Present Value Formula? – Find n in Future Value Formula!
- Balloon Balance for Loans
